TRANSFORMER.
| ideal transformer. |
Working principle of a transformer.
Transformer works on the principle of mutual induction of two coils or Faraday Law's Of Electromagnetic induction. When current in the primary coil is changed the flux linked to the secondary coil also changes. Consequently an EMF is induced in the secondary coil due to Faraday law's of electromagnetic induction.
Explanation
The transformer is based on two principles: first, that an electric current can produce a magnetic field (electromagnetism), and, second that a changing magnetic field within a coil of wire induces a voltage across the ends of the coil (electromagnetic induction). Changing the current in the primary coil changes the magnetic flux that is developed. The changing magnetic flux induces a voltage in the secondary coil.
The ideal transformer.
The ideal condition assumptions are:
- The windings of the transformer have negligible resistance thus there is no copper loss in the winding, no voltage drop
- Flux is confined within the core. Therefore, it is the same flux that links both the windings
- Permeability of the core is infinitely high which implies that a very small mmf (current) is required to set up the flux
- The core does not incur any hysteresis or eddy current loss. Hence, no core losses
Consider the ideal, lossless, perfectly-coupled transformer shown in the circuit diagram at right having primary and secondary windings with NP and NS turns, respectively.
The ideal transformer induces secondary voltage ES =VS as a proportion of the primary voltage VP = EP and respective winding turns as given by the equation
,
where,
- - VP/VS = EP/ES = a is the voltage ratio and NP/NS = a is the winding turns ratio, the value of these ratios being respectively higher and lower than unity for step-down and step-up transformers.
- - VP designates source impressed voltage,
- - VS designates output voltage, and,
- - EP & ES designate respective emf induced voltages.
According to the equation shown above, when the number of turns in the primary coil is greater than the number of turns in the secondary coil, the secondary voltage must be less than the primary voltage. On the other hand, when the number of turns in the primary coil is less than the number of turns in the secondary, the secondary voltage must be greater than the primary voltage.
Any load impedance  connected to the ideal transformer's secondary winding causes current to flow without losses from primary to secondary circuits, the resulting input and output apparent power therefore being equal as given by the equation
connected to the ideal transformer's secondary winding causes current to flow without losses from primary to secondary circuits, the resulting input and output apparent power therefore being equal as given by the equation
.
Combining the two equations yields the following ideal transformer identity
.
This formula is a reasonable approximation for the typical commercial transformer, with voltage ratio and winding turns ratio both being inversely proportional to the corresponding current ratio.
The load impedance  is defined in terms of secondary circuit voltage and current as follows
is defined in terms of secondary circuit voltage and current as follows
.
The apparent impedance  of this secondary circuit load referred to the primary winding circuit is governed by a squared turns ratio multiplication factor relationship derived as follows
of this secondary circuit load referred to the primary winding circuit is governed by a squared turns ratio multiplication factor relationship derived as follows
.
Induction law.
The transformer is based on two principles: first, that an electric current can produce a magnetic field and second that a changing magnetic field within a coil of wire induces a voltage across the ends of the coil (electromagnetic induction). Changing the current in the primary coil changes the magnetic flux that is developed. The changing magnetic flux induces a voltage in the secondary coil.
Referring to the two figures here, current passing through the primary coil creates a magnetic field. The primary and secondary coils are wrapped around a core of very high magnetic permeability, usually iron,so that most of the magnetic flux passes through both the primary and secondary coils. Any secondary winding connected load causes current and voltage induction from primary to secondary circuits in indicated directions.
The voltage induced across the secondary coil may be calculated from Faraday's law of induction, which states that:
where Vs = Es is the instantaneous voltage, Ns is the number of turns in the secondary coil, and dΦ/dt is thederivative of the magnetic flux Φ through one turn of the coil. If the turns of the coil are oriented perpendicularly to the magnetic field lines, the flux is the product of the magnetic flux density B and the area A through which it cuts. The area is constant, being equal to the cross-sectional area of the transformer core, whereas the magnetic field varies with time according to the excitation of the primary. Since the same magnetic flux passes through both the primary and secondary coils in an ideal transformer,the instantaneous voltage across the primary winding equals
Taking the ratio of the above two equations gives the same voltage ratio and turns ratio relationship shown above, that is,
.
The changing magnetic field induces an emf across each winding. The primary emf, acting as it does in opposition to the primary voltage, is sometimes termed the counter emf. This is in accordance with Lenz's law, which states that induction of emf always opposes development of any such change in magnetic field.
As still lossless and perfectly-coupled, the transformer still behaves as described above in the ideal transformer.
The real transformer.
Real transformer deviations from ideal.
The ideal model neglects the following basic linear aspects in real transformers:
- Core losses collectively called magnetizing current losses consisting of.
- Hysteresis losses due to nonlinear application of the voltage applied in the transformer core
- Eddy current losses due to joule heating in core proportional to the square of the transformer's applied voltage.
- Whereas the ideal windings have no impedance, the windings in a real transformer have finite non-zero impedances in the form of:
- Joule losses due to resistance in the primary and secondary windings
- Leakage flux that escapes from the core and passes through one winding only resulting in primary and secondary reactive impedance.
Leakage flux.
Main article: Leakage inductance
The ideal transformer model assumes that all flux generated by the primary winding links all the turns of every winding, including itself. In practice, some flux traverses paths that take it outside the windings. Such flux is termed leakage flux, and results in leakage inductance in series with the mutually coupled transformer windings. Leakage flux results in energy being alternately stored in and discharged from the magnetic fields with each cycle of the power supply. It is not directly a power loss (see Stray losses below), but results in inferior voltage regulation, causing the secondary voltage not to be directly proportional to the primary voltage, particularly under heavy load. Transformers are therefore normally designed to have very low leakage inductance. Nevertheless, it is impossible to eliminate all leakage flux because it plays an essential part in the operation of the transformer. The combined effect of the leakage flux and the electric field around the windings is what transfers energy from the primary to the secondary.
In some applications increased leakage is desired, and long magnetic paths, air gaps, or magnetic bypass shunts may deliberately be introduced in a transformer design to limit the short-circuit current it will supply. Leaky transformers may be used to supply loads that exhibit negative resistance, such as electric arcs, mercury vapor lamps, and neon signs or for safely handling loads that become periodically short-circuited such as electric arc welders.
Air gaps are also used to keep a transformer from saturating, especially audio-frequency transformers in circuits that have a DC component flowing in the windings.
Knowledge of leakage inductance is also useful when transformers are operated in parallel. It can be shown that if the percent impedance (Z) and associated winding leakage reactance-to-resistance (X/R) ratio of two transformers were hypothetically exactly the same, the transformers would share power in proportion to their respective volt-ampere ratings (e.g. 500 kVA unit in parallel with 1,000 kVA unit, the larger unit would carry twice the current). However, the impedance tolerances of commercial transformers are significant. Also, the Z impedance and X/R ratio of different capacity transformers tends to vary, corresponding 1,000 kVA and 500 kVA units' values being, to illustrate, respectively, Z ~ 5.75%, X/R ~ 3.75 and Z ~ 5%, X/R ~ 4.75.
Equivalent circuit.
See also: Steinmetz equivalent circuit
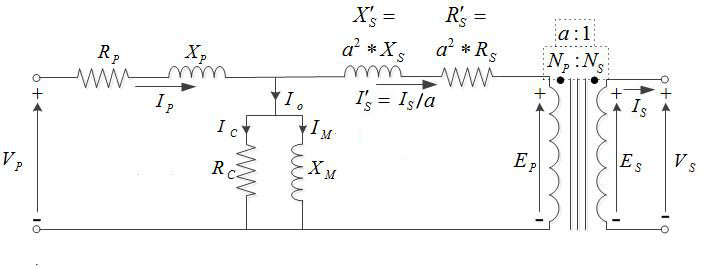
Referring to the diagram, a practical transformer's physical behavior may be represented by an equivalent circuit model, which can incorporate an ideal transformer.
Winding joule losses and leakage reactances are represented by the following series loop impedances of the model:
- Primary winding: RP, XP
- Secondary winding: RS, XS.
In normal course of circuit equivalence transformation, RS and XS are in practice usually referred to the primary side by multiplying these impedances by the turns ratio squared, (NP/NS) 2 = a2.
Core loss and reactance is represented by the following shunt leg impedances of the model:
- Core or iron losses: RC
- Magnetizing reactance: XM.
RC and XM are collectively termed the magnetizing branch of the model.
Core losses are caused mostly by hysteresis and eddy current effects in the core and are proportional to the square of the core flux for operation at a given frequency.The finite permeability core requires a magnetizing current IM to maintain mutual flux in the core. Magnetizing current is in phase with the flux, the relationship between the two being non-linear due to saturation effects. However, all impedances of the equivalent circuit shown are by definition linear and such non-linearity effects are not typically reflected in transformer equivalent circuits. With sinusoidal supply, core flux lags the induced emf by 90°. With open-circuited secondary winding, magnetizing branch current I0 equals transformer no-load current.
The resulting model, though sometimes termed 'exact' equivalent circuit based on linearity assumptions, retains a number of approximations. Analysis may be simplified by assuming that magnetizing branch impedance is relatively high and relocating the branch to the left of the primary impedances. This introduces error but allows combination of primary and referred secondary resistances and reactances by simple summation as two series impedances.
Transformer equivalent circuit impedance and transformer ratio parameters can be derived from the following tests: Open-circuit test, short-circuit test, winding resistance test, and transformer ratio test.
Basic transformer parameters and construction.
Effect of frequency.
Transformer universal emf equation
If the flux in the core is purely sinusoidal, the relationship for either winding between its rmsvoltage Erms of the winding, and the supply frequency f, number of turns N, core cross-sectional area a in m2 and peak magnetic flux density Bpeakin Wb/m2 or T (tesla) is given by the universal emf equation:[15]
If the flux does not contain even harmonics the following equation can be used for half-cycle average voltage Eavg of any waveshape:
The time-derivative term in Faraday's Law shows that the flux in the core is the integral with respect to time of the applied voltage.Hypothetically an ideal transformer would work with direct-current excitation, with the core flux increasing linearly with time. In practice, the flux rises to the point where magnetic saturation of the core occurs, causing a large increase in the magnetizing current and overheating the transformer. All practical transformers must therefore operate with alternating (or pulsed direct) current.
The emf of a transformer at a given flux density increases with frequency. By operating at higher frequencies, transformers can be physically more compact because a given core is able to transfer more power without reaching saturation and fewer turns are needed to achieve the same impedance. However, properties such as core loss and conductor skin effect also increase with frequency. Aircraft and military equipment employ 400 Hz power supplies which reduce core and winding weight.Conversely, frequencies used for some railway electrification systems were much lower (e.g. 16.7 Hz and 25 Hz) than normal utility frequencies (50 – 60 Hz) for historical reasons concerned mainly with the limitations of early electric traction motors. As such, the transformers used to step-down the high over-head line voltages (e.g. 15 kV) were much heavier for the same power rating than those designed only for the higher frequencies.
Operation of a transformer at its designed voltage but at a higher frequency than intended will lead to reduced magnetizing current. At a lower frequency, the magnetizing current will increase. Operation of a transformer at other than its design frequency may require assessment of voltages, losses, and cooling to establish if safe operation is practical. For example, transformers may need to be equipped with 'volts per hertz' over-excitation relays to protect the transformer from overvoltage at higher than rated frequency.
One example of state-of-the-art design is traction transformers used for electric multiple unit and high speed train service operating across the,country border and using different electrical standards, such transformers' being restricted to be positioned below the passenger compartment. The power supply to, and converter equipment being supply by, such traction transformers have to accommodate different input frequencies and voltage (ranging from as high as 50 Hz down to 16.7 Hz and rated up to 25 kV) while being suitable for multiple AC asynchronous motor and DC converters & motors with varying harmonics mitigation filtering requirements.
Large power transformers are vulnerable to insulation failure due to transient voltages with high-frequency components, such as caused in switching or by lightning.
Energy losses.
An ideal transformer would have no energy losses, and would be 100% efficient. In practical transformers, energy is dissipated in the windings, core, and surrounding structures. Larger transformers are generally more efficient, and those rated for electricity distribution usually perform better than 98%.
Experimental transformers using superconducting windings achieve efficiencies of 99.85%.The increase in efficiency can save considerable energy, and hence money, in a large heavily loaded transformer; the trade-off is in the additional initial and running cost of the superconducting design.
As transformer losses vary with load, it is often useful to express these losses in terms of no-load loss, full-load loss, half-load loss, and so on. Hysteresis and eddy current losses are constant at all loads and dominate overwhelmingly at no-load, variable winding joule losses dominating increasingly as load increases. The no-load loss can be significant, so that even an idle transformer constitutes a drain on the electrical supply and a running cost. Designing transformers for lower loss requires a larger core, good-quality silicon steel, or even amorphous steel for the core and thicker wire, increasing initial cost so that there is a trade-off between initial cost and running cost (also see energy efficient transformer).
Transformer losses arise from:
- Winding joule losses
- Current flowing through winding conductors causes joule heating. As frequency increases, skin effect and proximity effect causes winding resistance and, hence, losses to increase.
- Core losses
-
- Hysteresis losses
- Each time the magnetic field is reversed, a small amount of energy is lost due to hysteresis within the core. According to Steinmetz's formula, the heat energy due to hysteresis is given by
, and,
- hysteresis loss is thus given by
- where, f is the frequency, η is the hysteresis coefficient and βmax is the maximum flux density, the empirical exponent of which varies from about 1.4 to 1 .8 but is often given as 1.6 for iron.
- Eddy current losses
- Ferromagnetic materials are also good conductors and a core made from such a material also constitutes a single short-circuited turn throughout its entire length. Eddy currents therefore circulate within the core in a plane normal to the flux, and are responsible for resistive heating of the core material. The eddy current loss is a complex function of the square of supply frequency and inverse square of the material thickness. Eddy current losses can be reduced by making the core of a stack of plates electrically insulated from each other, rather than a solid block; all transformers operating at low frequencies use laminated or similar cores.
- Magnetostriction related transformer hum
- Magnetic flux in a ferromagnetic material, such as the core, causes it to physically expand and contract slightly with each cycle of the magnetic field, an effect known as magnetostriction, the frictional energy of which produces an audible noise known as mains hum or transformer hum. This transformer hum is especially objectionable in transformers supplied at power frequencies and in high-frequency flyback transformers associated with PAL system CRTs.
- Stray losses.
- Leakage inductance is by itself largely lossless, since energy supplied to its magnetic fields is returned to the supply with the next half-cycle. However, any leakage flux that intercepts nearby conductive materials such as the transformer's support structure will give rise to eddy currents and be converted to heat.There are also radiative losses due to the oscillating magnetic field but these are usually small.
- Mechanical vibration and audible noise transmission.
- In addition to magnetostriction, the alternating magnetic field causes fluctuating forces between the primary and secondary windings. This energy incites vibration transmission in interconnected metalwork, thus amplifying audible transformer hum.
Core form and shell form transformers.
Closed-core transformers are constructed in 'core form' or 'shell form'. When windings surround the core, the transformer is core form; when windings are surrounded by the core, the transformer is shell form. Shell form design may be more prevalent than core form design for distribution transformer applications due to the relative ease in stacking the core around winding coils. Core form design tends to, as a general rule, be more economical, and therefore more prevalent, than shell form design for high voltage power transformer applications at the lower end of their voltage and power rating ranges (less than or equal to, nominally, 230 kV or 75 MVA). At higher voltage and power ratings, shell form transformers tend to be more prevalent.Shell form design tends to be preferred for extra high voltage and higher MVA applications because, though more labor intensive to manufacture, shell form transformers are characterized as having inherently better kVA-to-weight ratio, better short-circuit strength characteristics and higher immunity to transit damage.





No comments:
Post a Comment